 By Medium -
2020-11-29
By Medium -
2020-11-29
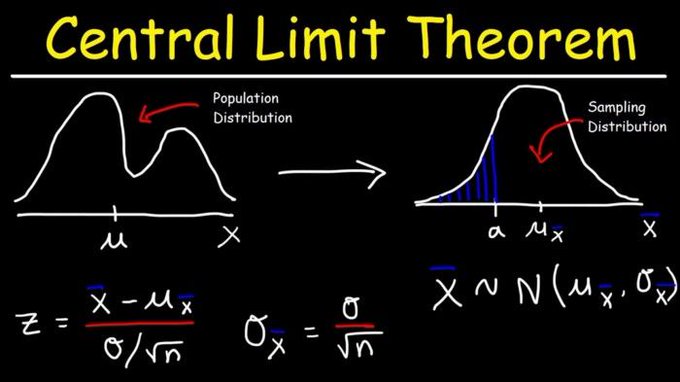
Note: Here I will try to cover the idea of the Central Limit Theorem, and it’s significance in statistical analysis, and how it is useful…
 By Medium -
2020-12-10
By Medium -
2020-12-10
A/B testing is a tool that allows to check whether a certain causal relationship holds. For example, a data scientist working for an e-commerce platform might want to increase the revenue by…
 By DataCamp Community -
2021-02-05
By DataCamp Community -
2021-02-05
PYTHON for FINANCE introduces you to ALGORITHMIC TRADING, time-series data, and other common financial analyses!
 By R-bloggers -
2019-05-22
By R-bloggers -
2019-05-22
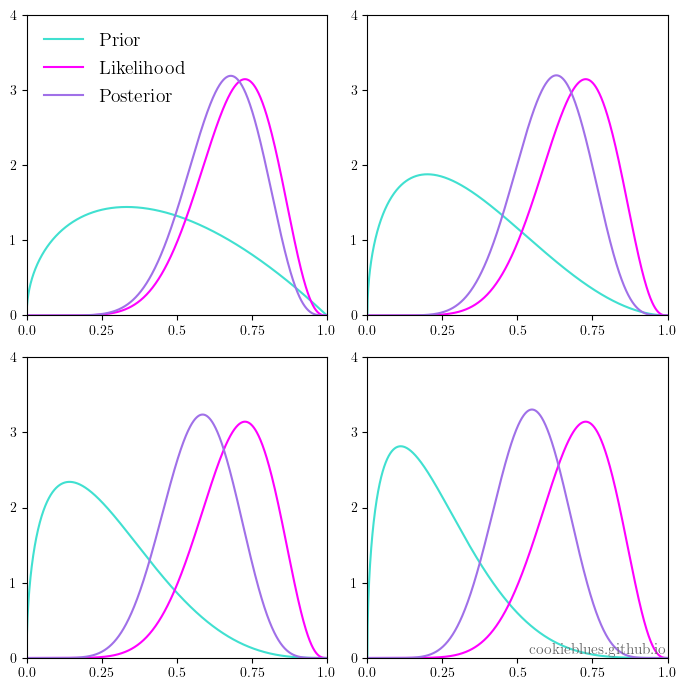
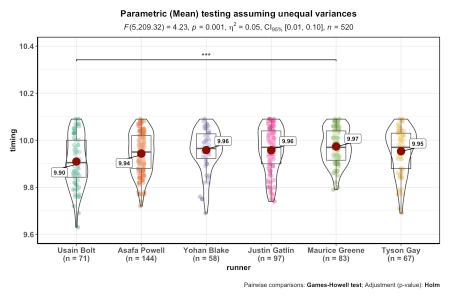
So, a programmer, a frequentist, and a bayesian walk into a bar. No this post isn’t really on the path to some politically incorrect ste ...
 By PyImageSearch -
2021-02-08
By PyImageSearch -
2021-02-08
In this tutorial, you will learn how to perform histogram matching using OpenCV and scikit-image.
 By realpython -
2021-02-25
By realpython -
2021-02-25
In this tutorial, you'll learn everything you need to know to get up and running with NumPy, Python's de facto standard for multidimensional data arrays. NumPy is the foundation for most data science ...