By 9elements Blog -
2021-01-04
Learn how to build an algorithmic layout that switches from two centered elements to a spaced-out flex layout.
By Distill -
2021-02-27
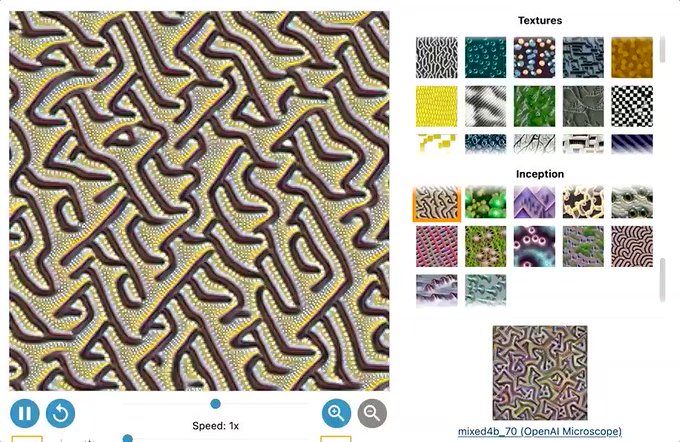
Neural Cellular Automata learn to generate textures, exhibiting surprising properties.
By Science -
2020-12-31
Long before anyone knew of SARS-CoV-2, a small band of government and university scientists uncovered a prototypical key that unlocked life-saving immunizations.
By GeekyAnts Tech Blog -
2021-03-03
Flight Simulator, Heard Of It?
You might know about Microsoft's Flight Simulator release in August last year and like me, if you're interested in flight simulators or photorealistic recreations of rea
By realpython -
2020-12-15
Once you learn about for loops in Python, you know that using an index to access items in a sequence isn't very Pythonic. So what do you do when you need that index value? In this tutorial, you'll lea ...
By joshwcomeau -
2020-12-11
“Margin collapse” has a dastardly reputation, one of the trickier parts of CSS. Fortunately, it gets a lot easier once you learn a few rules! In this tutorial, we take a deep dive into the governing p ...
